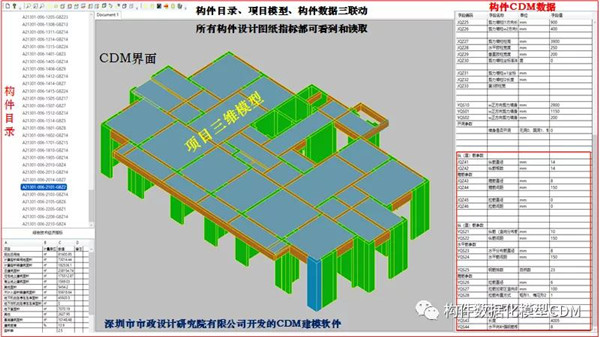
BIM数学模型通过计算机图形学可以转换为BIM三维模型,由BIM数学模型表达的CDM三维建模软件界面更友好,CDM数据与三维建模和工程应用软件无缝连接。构件、模型、构件数据三者联动,构件数据及查询方式符合工程习惯和图纸语言:
1、计算机图形学
计算机图形学(Computer Graphics,简称CG)是一种使用数学算法将二维或三维图形转化为计算机显示器的栅格形式的科学。简单地说,计算机图形学的主要研究内容就是研究如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法。
计算机图形学进入我国大概在上个世纪70年代末和80年代初,那时国内还没有计算机学科。于是,开始学习和研究计算机图形学的大部分都是搞数学的一些学者和教授。由此可见,计算机图形学是需要数学知识较多的一门计算机应用技术学科,在我国也是应用数学的一个重要分支。计算机图形学里面用到的数学比较多,包括:微积分、线性代数、矩阵计算、微分几何、数值计算和分析、计算方法、偏微分方程、微分方程数值解、最优化、概率、统计、计算几何等。
因此,数学是计算机图形学的基础。
计算机图形学主要包含四大部分的内容:建模(Modeling)、渲染(Rendering)、动画(Animation)和人机交互(Human–computer Interaction, HCI)。
(1)建模(Modeling)
要在计算机中表示一个三维物体,首先要有它的几何模型表达。因此,三维模型的建模是计算机图形学的基础,是其他内容的前提。表达一个几何物体可以是用数学上的样条函数或隐式函数来表达;也可以用光滑曲面上的采样点及其连接关系所表达的三角网格来表达(即连续曲面的分片线性逼近)。
目前物体的建模方法,大体上有三种:第一种方式利用三维软件建模;第二种方式通过仪器设备测量建模;第三种方式利用图像或者视频来建模。
(2)渲染(Rendering)
有了三维模型或场景,怎么把这些三维几何模型画出来,产生令人赏心悦目的真实感图像?这就是传统的计算机图形学的核心任务,在计算机辅助设计,影视动漫以及各类可视化应用中都对图形渲染结果的高真实感提出了很高的要求。
(3)动画(Animation)
动画是采用连续播放静止图像的方法产生物体运动的效果。计算机动画借助于编程或动画制作软件生成一系列的景物画面,是计算机图形学的研究热点之一。研究方向包括:人体动画,关节动画,运动动画,脚本动画,具有人的意识的虚拟角色的动画系统等。另外,高度物理真实感的动态模拟,包括对各种形变、水、气、云、烟雾、燃烧、爆炸、撕裂、老化等物理现象的真实模拟,也是动画领域的主要问题。这些技术是各类动态仿真应用的核心技术,可以极大地提高虚拟现实系统的沉浸感。计算机动画的应用领域广泛,比如动画片制作,广告、电影特技,训练模拟,物理仿真,游戏等。
(4)人机交互(Human–computer Interaction, HCI)
人机交互是指人与计算机之间以一定的交互方式或交互界面,来完成确定任务的人与计算机之间的信息交换过程。简单来讲,就是人如何通过一定的交互方式告诉计算机来完成他所希望完成的任务。
2、计算机图形学的应用领域
CAD是计算机图形学在工业界最广泛、最活跃的应用领域。计算机图形学被用来进行土建工程、机械结构和产品的设计,包括设计飞机、汽车、船舶的外形和发电厂、化工厂等的布局以及电子线路、电子器件等。有时,着眼于产生工程和产品相应结构的精确图形,然而更常用的是对所设计的系统、产品和工程的相关图形进行人——机交互设计和修改,经过反复的迭代设计,便可利用结果数据输出零件表、材料单、加工流程和工艺卡,或者数据加工代码的指令。
CAD领域另一个非常重要的研究领域是基于工程图纸的三维形体重建。三维形体重建就是从二维信息中提取三维信息,通过对这些信息进行分类、综合等一系列处理,在三维空间中重新构造出二维信息所对应的三维形体,恢复形体的点、线、面及其拓扑关系,从而实现形体的重建。二维图纸设计在工程界中仍占有主导地位,工程上有大量的旧的透视图和投影图片可以利用、借鉴,许多新的设计可凭借原有的设计基础做修改即可完成。同时三维几何造型系统,因为可以做装配件的干涉检查以及有限元分析、仿真、加工等后续操作,代表CAD技术的发展方向。目前主要的三维形体重建算法是针对多面体和对主轴方向有严格限制的二次曲面体的。任意曲面体的三维形体重建,至今仍是一个未解决的世界难题。
随着计算机网络的发展,在网络环境下进行异地异构系统的协同设计,已经成为CAD领域最热门的课题之一。
现代产品设计已不再是一个设计领域内孤立的技术问题,而是综合了产品各个相关领域、相关过程、相关技术资源和相关组织形式的系统化工程。它要求设计团队在合理的 组织结构下,采用群体工作方式来协调和综合设计者的专长,并且从设计一开始就考虑产品生命周期的全部因素,从而达到快速响应市场需求的目的,协同设计的出现使企业生产的时空观发生了根本的变化。使异地设计、异地制造、异地装配成为可能,从而为企业在市场竞争中赢得了宝贵的时间。
3、BIM三维模型与计算机图形学
Revit建模软件的模型图元(Model Elements)生成建筑物几何模型,表示物理对象的各种图形元素,代表着建筑物的各类构件。模型图元是构成Revit信息模型最基本的图元,也是模型的物质基础。分为两类:主体图元(HostElements)和构件图元(Component Elements)
主体图元:可以在模型中承纳其它模型图元对象的模型图元,代表着建 筑物中建造在主体结构中的构件。如:柱、梁、楼板、墙体、屋顶、天花板、楼梯等
构件图元:除主体图元之外的所有图元。一般在模型中不能够独立存在 ,必须依附主体图元才可以存在。如门、窗、上下水管道、家俱等
构件,一个建筑物是由许多构件组成的。如墙、楼板、梁、柱、门 ,在Revit称之为图元。构件不仅仅指墙、门、窗等具体的建筑构件,还包括文字注释、尺寸标注、标高等属于某种具体的图元类型。这是与以往CAD软件不同之处。放置在建筑模型中的所有对象都属于某一种类别,这种广泛的类别可以进一步细分为“族”,对象类型还可以分解成子类别。例:项目中所有的门属于“门类别”。在Revit中每一个对象都附带有自己的属性参数。
“实例”是放置在项目中的实际项,在建筑(模型实例)或图纸(注释实例)中有特定的位置。实例是族中类型的具体例证,是类型模型的具体化。实例是唯一的,但任何类型可以有许多相同的实例,在设计中定义在不同的部位。
标准构件族是在建筑设计中使用的标准尺寸和配置的常见构件和符号。可以使用族编辑器,标准族样板来定义族的几何图形和尺寸。
从上述计算机图形学的研究内容和应用领域对照Revit建模软件可见,目前我们所认识的BIM三维模型属于计算机图形学范畴。因此,BIM三维模型强调了可视化、协调性、模拟性、优化性、可出图的BIM的五大特点。
4、BIM数学模型与BIM三维模型
图形学的基础之一就是计算几何,没有理论数学那么高深莫测,它很有实践性,有时候甚至可以简单到匪夷所思。计算几何是随着计算机和CAD的应用而诞生的一门新兴学科,在国外被称为“计算机辅助几何设计(ComputerAided Geometric Design,CAGD)”。三维模型建模(Modeling)是计算机图形学的基础,是渲染、动画、人机交互的前提。
表达一个几何物体可以是用数学上的样条函数或隐式函数来表达;也可以用光滑曲面上的采样点及其连接关系所表达的三角网格来表达(即连续曲面的分片线性逼近)。我们将按此数学方式表达的几何物体称为几何数学模型。
计算机图形学就是使用数学算法将几何数学模型转化为在计算机中表示的几何图形(几何三维模型)、以及利用计算机进行图形的计算、处理和显示的相关原理与算法。
由此可见,几何数学模型与几何三维模型可以独立存在,因此,BIM的数学模型可以表达为式(1):
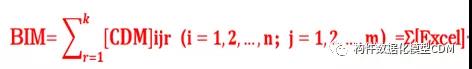
式中:(i,j,r)为构件id,确定了构件特征点在建筑物中的坐标;
CDM:构件数据化模型,确定了构件几何及表面形状、非几何参数。
(1)三维模型的基本参数
在计算机图形学中,矩形占有重要位置。窗口、视区、屏幕客户区等都是矩形。正确定义好矩形,是计算机图形学的入门。常用的矩形定义方式有两种:
(1)使用左上角点与右下角点定义矩形
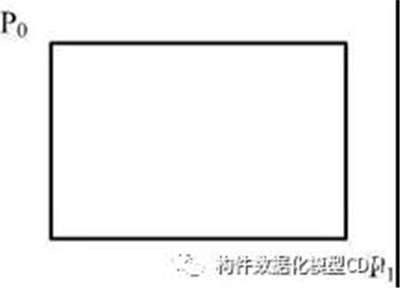
图1
这是矩形的常规定义,使用左上角点P1和右下角点P2可以计算出矩形的宽度和长度以及中心点坐标。
(2)使用中心点与半宽和半高定义窗口
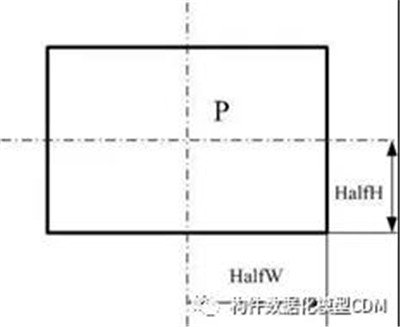
图2
这种定义一般用于碰撞检测中,很方便判断两个矩形块(管道)是否发生碰撞,或者矩形块是否与客户区边框是否发生碰撞。利用计算机图形学算法我们可以判断一个点是否在矩形、圆形及任何指定的图形内。这也是BIM软件碰撞检查的基本算法。
(2)BIM数学模型与BIM三维模型
式(1)表达的BIM数学模型,将构件的三维数据以图2(加构件长度)方式描述,几何及非几何参数均纳入CDM标准中,CDM标准以元数据方式表述。这样,任何建模软件和其他软件都可以轻易读写BIM数学模型,实现所有应用软件信息共享。
BIM三维模型在BIM数学模型基础上完成可视化、协调性、模拟性、优化性、可出图等。BIM数学模型解决BIM信息共享问题,BIM信息应用交给BIM软件、CAD软件及各种建筑业应用软件。这大大降低了BIM的实现难度。
BIM数学模型是建筑业的数据中台,以此为起点,我们会创新出各种BIM应用。重要的是,从以前看似枯燥的数学到看到它的实际应用的过程中,你会更容易享受数学的美妙。在你不断进行BIM数学模型的研究的程中,你会感觉到你的数学知识越来越不够用,从而真正理解其中的数学思想和数学方法。
在大学里,你所学的那些数学看起来都很抽象,枯燥无味,这是因为你并不知道它们的用处,甚至连讲课的老师也不知道,而你的目的只是记住那些定理和公式,考个好分数。与大学学习数学不一样的是,你在BIM数学模型的学习和研究过程中会感受到数学的用处和美妙,这时你学习数学的目的将更加明确,兴趣将更加浓厚,学习方法将更加有效。因为你是在使用数学的过程中在学习数学。常用的数学课程你不必都要熟悉,许多研究工作者从不需要考虑其中提到的某些数学知识,成功的研究者总是将某一方面的数学知识和数学工具用到极致。
益韧BIM培训小编认为:研究与应用BIM数学模型需要“数形结合”,要有图形的想象能力;数学公式不重要,是“纸老虎”,重要的是背后的思想及其所表达的概念,公式只是它们的一个抽象表达;活到老,学到老。要创新就要不断学习新的知识和技术,使自己不断进步和增长功力,才是王道。